How Many Degrees Is a Triangle

Triangles are one of the most fundamental shapes in geometry. They are simple yet complex, and their properties have fascinated mathematicians for centuries. One of the most intriguing aspects of a triangle is its degree measurement, which refers to the sum of its three angles. This seemingly straightforward concept has many implications and applications in mathematics and beyond. In this article, we will explore the degrees of a triangle, including how they are calculated, their relationship to the sides of a triangle, and the different types of triangles that exist based on their degree measurements. By the end of this article, you will have a deeper understanding of this essential geometric shape and its properties.

The Three Sides of a Triangle

When we think of a triangle, the first thing that comes to mind is its three sides. The sides of a triangle are the straight lines that connect its three vertices or corners. Each side has two endpoints, and they are named using the letters of the vertices they connect. For example, if a triangle has vertices A, B, and C, then its sides can be named AB, BC, and AC.

It’s important to note that in any triangle, no two sides can be parallel. Additionally, the sum of any two sides must always be greater than the length of the third side. This is known as the Triangle Inequality Theorem and it helps us determine whether a set of three lengths can form a valid triangle or not. Understanding these basic properties of triangles is crucial for further exploring their angles and relationships between them.

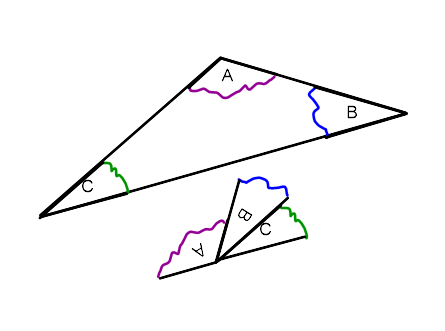
The Three Angles of a Triangle

When we think of a triangle, we often picture the three sides that make up its shape. However, it’s important to also consider the angles within the triangle. A triangle has three angles, and their measurements can tell us a lot about the shape of the triangle.

The sum of the three angles in any triangle is always 180 degrees. This means that no matter what size or shape a triangle is, its angles will always add up to 180 degrees. Additionally, each angle within a triangle is named based on its position relative to the sides. The angle opposite to the longest side is called the “hypotenuse,” while the other two angles are referred to as “base angles.”

Understanding the measurements and relationships between these angles can help us classify triangles and solve geometric problems involving them. In fact, knowing just two of a triangle’s angle measurements allows us to determine the third one using basic algebraic equations. So while it may be easy to overlook them at first glance, understanding the three angles of a triangle is crucial for anyone studying geometry or working with shapes in real-world applications.

The Relationship Between the Sides and Angles of a Triangle

When it comes to triangles, there is a close relationship between the sides and angles of the shape. In fact, this relationship is what makes triangles such an interesting and important part of geometry.

One of the most important relationships between the sides and angles of a triangle is known as the Law of Cosines. This law states that in any triangle, the square of one side is equal to the sum of the squares of the other two sides minus twice their product times the cosine of their included angle. This may sound complicated at first, but it essentially means that we can use trigonometry to find missing sides or angles in a triangle when we know some information about its other parts.

Another important relationship between sides and angles in a triangle is known as the Law of Sines. This law states that for any triangle, the ratio of each side length to its opposite angle’s sine value is constant. Again, this may sound complex, but it allows us to solve for unknowns in a triangle using only basic trigonometric functions.

Understanding these relationships between sides and angles is crucial for solving problems involving triangles, from finding missing measurements to determining whether two shapes are congruent or similar. By mastering these concepts, you’ll be well on your way to becoming a true geometry expert!

Properties of Triangles

When it comes to triangles, there are a few important properties that we need to keep in mind. Firstly, the sum of the three angles in any triangle always adds up to 180 degrees. This means that if we know two of the angles, we can easily calculate the third. Additionally, the side opposite to the largest angle is always the longest side of the triangle.

Another important property of triangles is that they can be classified based on their sides and angles. Equilateral triangles have three equal sides and three equal angles of 60 degrees each. Isosceles triangles have two equal sides and two equal angles, while scalene triangles have no equal sides or angles.

Finally, it’s worth noting that triangles can also be used to represent other shapes and objects. For example, a right-angled triangle with one angle measuring 90 degrees can be used to calculate distances and heights using trigonometry. Understanding these properties of triangles is essential for solving problems related to geometry and mathematics in general.

Types of Triangles

There are several types of triangles that we can classify based on their properties. One way to classify triangles is by their sides. An equilateral triangle has three equal sides, while an isosceles triangle has two equal sides and one different side. A scalene triangle has three different sides.

Another way to classify triangles is by their angles. An acute triangle has three angles less than 90 degrees, while a right triangle has one angle measuring exactly 90 degrees. Finally, an obtuse triangle has one angle greater than 90 degrees.

We can also combine these classifications to get more specific types of triangles, such as an equilateral and acute triangle or an isosceles and obtuse triangle. Understanding the different types of triangles can help us solve problems involving them and appreciate the unique properties each type possesses.

Conclusion

In conclusion, triangles are fascinating shapes that have been studied for centuries. They are defined by their three sides and three angles, which have a unique relationship with each other. The sum of the interior angles of any triangle is always 180 degrees, regardless of its size or shape. This property allows us to calculate missing angles in a triangle using simple algebraic equations. Additionally, there are various types of triangles based on their side lengths and angle measures, such as equilateral, isosceles, scalene, acute, obtuse, and right triangles. Understanding the properties and types of triangles can help us solve real-world problems in fields like architecture, engineering, and physics. Whether you’re a student learning geometry or a professional working with shapes every day, knowing how many degrees a triangle has is an essential piece of knowledge that will serve you well throughout your life.